Пошук площі трикутника — одне з тих завдань, яке зустрічається не лише у шкільних підручниках, але й у реальному житті: під час ремонту, планування ділянки чи навіть у творчих проєктах. На щастя, для цього не потрібно бути генієм математики. Існує кілька простих та зрозумілих формул, кожна з яких стане у пригоді за певних умов.
Давайте розберемо найпопулярніші методи, які допоможуть вам швидко та легко обчислити площу будь-якого трикутника, незалежно від того, які дані у вас є.
Класичний метод: через основу та висоту
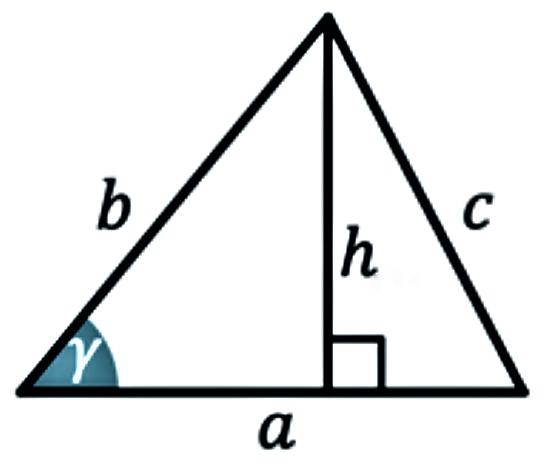
Це, мабуть, найвідоміша і найпростіша формула, яку пам’ятають ще зі школи. Вона ідеально підходить, коли ви знаєте довжину однієї зі сторін трикутника та довжину висоти, проведеної до цієї сторони.
Формула: S = ½ × a × h
Де:
- S — це площа трикутника.
- a — довжина сторони трикутника (основи).
- h — висота, опущена на цю сторону.
Висота — це перпендикуляр, проведений з вершини трикутника до протилежної сторони (або до її продовження).
Простий приклад:
Уявіть, що у вас є трикутник, довжина основи якого становить 10 см, а висота, проведена до неї, — 6 см.S = ½ × 10 см × 6 см = 30 см²
Площа цього трикутника дорівнює 30 квадратних сантиметрів. Все дуже просто!
Цей метод універсальний і підходить для будь-якого типу трикутника: гострокутного, тупокутного чи прямокутного. Головне — мати значення основи та відповідної висоти.
Коли відомі дві сторони та кут між ними
Що робити, якщо висота невідома, але ви знаєте довжини двох сторін і величину кута між ними? Для цього існує інша зручна формула, яка використовує тригонометрію, а саме — синус кута.
Формула: S = ½ × a × b × sin(α)
Де:
- a і b — довжини двох сусідніх сторін.
- sin(α) — синус кута α, що лежить між цими сторонами.
Значення синуса для найпоширеніших кутів можна знайти у тригонометричних таблицях або порахувати на калькуляторі.
| Кут (α) | sin(α) |
|---|---|
| 30° | 0.5 |
| 45° | ≈ 0.707 |
| 60° | ≈ 0.866 |
| 90° | 1 |
Приклад застосування:
Припустимо, є трикутник зі сторонами 8 см і 12 см, а кут між ними становить 30°.
S = ½ × 8 см × 12 см × sin(30°)
S = ½ × 8 × 12 × 0.5 = 24 см²
Цей метод особливо корисний у геодезії та проєктуванні, де часто вимірюють саме сторони та кути.
Формула Герона: коли відомі всі три сторони
Іноді єдине, що ми знаємо про трикутник, — це довжини всіх трьох його сторін. Висоту чи кути виміряти неможливо. У такому випадку на допомогу приходить формула Герона, названа на честь давньогрецького математика. Вона може виглядати трохи складною, але насправді є дуже логічною.
Формула: S = √[p(p-a)(p-b)(p-c)]
Для початку потрібно знайти півпериметр (p):
p = (a + b + c) / 2
Де:
- a, b, c — довжини трьох сторін трикутника.
- p — півпериметр.
- √ — знак квадратного кореня.
Порада: Цей метод є універсальним для будь-якого трикутника, якщо відомі всі його сторони. Він рятує, коли інші способи неможливо застосувати.
Давайте розрахуємо на прикладі:
Маємо трикутник зі сторонами 13 см, 14 см і 15 см.
- Знаходимо півпериметр (p):
p = (13 + 14 + 15) / 2 = 42 / 2 = 21 см - Підставляємо значення у формулу Герона:
S = √[21 × (21-13) × (21-14) × (21-15)]
S = √[21 × 8 × 7 × 6]
S = √7056
S = 84 см²
Отже, площа трикутника дорівнює 84 квадратних сантиметри.
Вибір правильного інструменту для завдання
Як бачите, не існує єдиного «правильного» способу знайти площу трикутника. Вибір методу залежить виключно від того, які дані у вас є.
- Знаєте основу і висоту? Використовуйте класичну формулу.
- Відомі дві сторони і кут між ними? Формула з синусом — ваш найкращий вибір.
- Маєте всі три сторони? Формула Герона прийде на допомогу.
Розуміння цих трьох основних підходів дозволить вам впоратися з будь-яким завданням, пов’язаним із площею трикутника, будь то шкільна задача чи практична потреба в побуті.

Автор та редактор